Statistik

Tillsammans med ekonomi är statistik ett lätt område när det gäller att hitta tydliga tillämpningar av matematiken eftersom det är så universellt förekommande. Vi ska i detta kapitel fördjupa oss i hur statistiska undersökningar går till, vad man kan dra för slutsatser och hur man tänker kritiskt kring dessa.

Dessutom ska vi tala om något som oftast är mycket roligare, hur undersökningar inte ska gå till och hur statistik absolut inte ska presenteras. Tidningar och annan media är full av olika statistiska undersökningar och då är det oerhört viktigt för oss alla att vi kan tolka och förstå dem på ett korrekt sätt. För den som arbetar med praktisk statistik är det särskilt dåligt att inte vara tillräckligt insatt i metoderna. Det är också viktigt för oss andra att förstå när det inte går att dra några slutsatser och förstå när någon försöker vilseleda oss. Tycker du inte att detta brukar hända särskilt ofta är detta kapitel kanske ännu viktigare för dig.

Området sannolikhetsteori som idag är centralt för statistiken dök först upp under 1500-talet när bland annat tärningsspel blev populärt och många människor började förlora stora summor pengar. De ville veta varför och vad som kunde göras för att balansera sina spel. Ämnet mognade till en strikt logiskt definierad gren av matematiken under 1900-talet. Det används idag för beräkningar av odds för vadslagning inom exempelvis boll- och hästsporter (se mer under kapitlet Sport och spel).

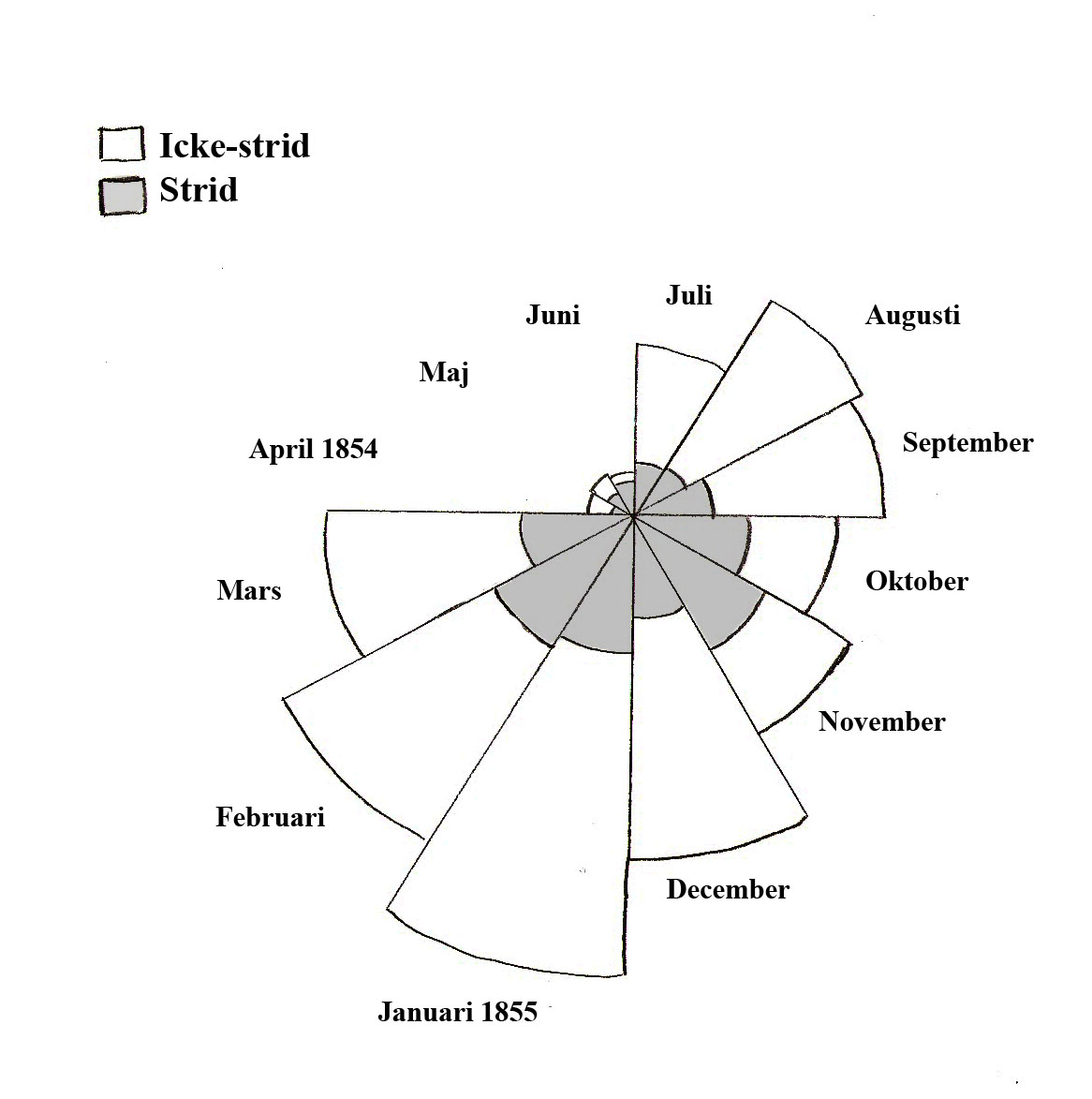
Florence Nightingale revolutionerade under 1800-talet det medicinska området genom att visa hur sjukdomar kunde bekämpas med noggranna observationer och statistik. Ett berömt diagram av henne visas nedan och beskriver orsaker till dödsfall. Hon visade att majoriteten av dödsfallen i krig inte ägde rum i strid och kunde motverkas med till exempel bättre hygien.

Användandet av matematisk statistik är idag ett krav före lansering av alla läkemedel. Läkemedelstester utformas med en testgrupp och en kontrollgrupp, där bara den första får behandlingen medan den andra ges något annat. Detta för att se om den aktuella behandlingen faktiskt har någon effekt eller om resultaten kan bero på någon annan faktor. Samtidigt är det viktigt att få chansen att kartlägga hur vanliga olika bieffekter är.

Forskning i matematisk statistik har bland många andra viktiga resultat visat att test ger mest rättvisa resultat om kontroll- och testgrupper är lika stora, vilket är viktigt att veta vid utformningen av dem. I verkligheten måste dessa anpassas efter olika risker som också beräknas matematiskt (området riskanalys). Nära läkemedelsforskning ligger också forskning om genetik och smittospridning som båda nödgar matematiska kunskaper.

Andra studieområden berör hur molekyler i olika gaser gör sin till synes slumpmässiga rörelse, idag kallat Brownsk rörelse efter att biologen Robert Brown först analyserat detta, följd av bland andra Bertrand Russell och Albert Einstein. Slumpmässighet är något som människor i allmänhet är dåliga på att efterhärma och det finns därför goda tester för att kontrollera om uppmätta data från exempelvis en statistisk undersökning kan misstänkas ha falsifierats.

Kvantmekanik är en gren av fysiken som är uppbyggd på sannolikhetsteorins grunder. Den behandlar de allra minsta partiklarna och är grunden för modern kemi såsom utvecklingen av nya material och förståelsen av olika kemiska reaktioner. I framtiden kan kvantfysiken förhoppningsvis också hjälpa oss konstruera en helt ny typ av dator, kvantdatorn, med beräkningshastigheter långt över vad som är möjligt idag.

En statistisk undersökning

En undersökning görs för att ta reda på något. Det kan ha med samhället att göra: hur populärt ett politiskt parti eller en TV-serie är, eller att bestämma den förväntade livslängden hos en viss befolkning. I det första fallet genomförs någon form av intervju, i det andra fallet är det data som redan finns tillgänglig som analyseras. En undersökning kan också äga rum i mer kontrollerade former, till exempel i laboratorier, vilket vi diskuterar närmare i nästa del.

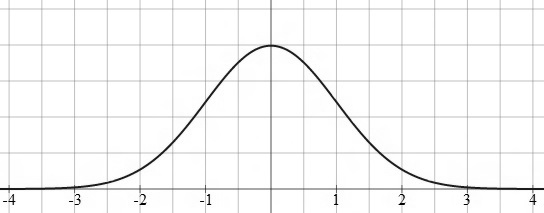
Ett begrepp som från och med 2011 ingår i gymnasieutbildningen är normalfördelningen. Det är en matematisk funktion definierad på följande vis:

\[ 1 / {σ √{2π} } e^{-{(x-σ)^2} / {2 σ^2} } \]

Normalfördelningens graf har ett utseende som påminner om en gammaldags ringklocka och går därför under namnet ”klockkurvan”. Den kan se ut såhär:

När en undersökning genomförs bland människor kan man som undersökare (nästan) alltid utgå ifrån att inte alla inblandade kan tillfrågas. Att se exakt hur populärt ett parti är i Sverige skulle kräva att vi frågade och fick ett ärligt svar från alla, men då rör det sig om strax över sju miljoner människor (Antalet röstberättigade inför allmänna valet 2010 enligt Valmyndighetens hemsida). Om femtio människor jobbade åtta timmar per vardag med att bara fråga folk skulle det ta alltför lång tid! Låt oss säga att de behöver 30 sekunder per intervjuperson. Hur lång tid skulle undersökningen ta? Antalet sekunder på en jobbvecka är 5 veckodagar gåner 8 timmar gånger 60 minuter per timme gånger 60 sekunder per minut, lika med 144 000.

Detta multiplicerat med 50 (arbetande människor) delat med 30 (sekunder per fråga) ger oss bara 240 000 frågade personer per vecka. Vi kommer behöva över ett halvår för att fråga alla miljontals människor. Under denna långa tidsperiod kan opinionen redan ha hunnit svänga märkvärt, vilket gör undersökningen värdelös.

Det finns andra praktiska skäl till att undersökningar inte genomförs på detta vis. Sällan vill alla ställa upp. Vissa personer kan vara svåra eller omöjliga att få tag på för att erhålla ett svar. Istället gör man ett urval: en bråkdel väljs slumpvis ut, kanske 7000. Med detta urval försöker man göra en så bra representation som möjligt av hela folkgruppen som undersökningen gäller. Andelen av olika åldrar, etniciteter och bakgrunder ska vara lika stor i befolkningen som i urvalsgruppen. Representeras inte befolkningen väl av urvalet, oftast på grund av att det är alldeles för litet, kallas det skevt. Fler tillfrågade är alltid bättre, så länge urvalet inte blir mer skevt, vilket sker då intervjuare tillfrågar extra många av en viss befolkningsgrupp men utesluter andra.

Undersökningar genomförs ständigt och i allt större utsträckning av internetföretag som Google och Facebook för att kartlägga och sammanställa så mycket information de kan om sina användare. Avsikten är att göra de annonser som visas så relevanta som möjligt. På så vis tjänar de pengar på sina tjänster. Undersökningen utförs inte med hjälp av frågor utan genom lagring av dina vanor, söktermer, vilka andra annonser du klickat på, och så vidare.

Göra en uppskattning

När någon genomför en undersökning finns det ett visst värde som ska uppskattas, eller kortare sagt skatta. I exemplet ovan är det antalet människor som tänkt rösta på ett visst parti som ska skattas. Andelen personer är alltså det intressanta, enligt principen att om 700 av de 7000 tillfrågade vill rösta för ett visst parti, så kommer ungefär lika stor andel (10 %) av hela befolkningen också rösta så.

Självklart görs vissa antaganden, framför allt att alla talar sanning. Det är ett tvunget antagande man som intervjuare tyvärr inte kommer ifrån. Vi säger egentligen att ungefär 10 % av befolkningen borde ha samma partisympati. Notera de osäkra orden. Vi vet inte hur skevt vårt urval är och det sanna värdet borde ligga någonstans omkring 10 procent. Kan vi göra någon form av beräkning av hur nära vi förmodligen är? Svaret är ja, och involverar vad som kallas konfidensintervall.

En uppskattning kan ses som ett ungefärligt svar på frågan ”hur många?”. Trots att skattningen ger ett visst svar är det högst ungefärligt och det är viktigt att kunna säga något om noggrannhetsordningen, hur stort felet sannolikt är.

Låt oss säga att undersökningen hävdar att 10 % av befolkningen tänkt rösta på ett parti A. Det verkliga värdet ligger då inom ett intervall centrerat kring vad vi mätt upp. Hur långt ifrån 10 det sanna värdet är kan vi inte veta säkert, men med en viss säkerhetsnivå kan vi bestämma ett intervall det troligen ligger inom. Vi blir aldrig 100 % säkra.

Ett konfidensintervall med 95 % säkerhet är vanligt. För 99,9 % säkerhet blir intervallen större, men vi kan vara mycket säkrare att det sanna värdet finns med. Ju fler mätningar som genomförs desto mindre blir intervallen. Därför är det alltid bra att fråga så många som möjligt. Intervallen blir mindre eftersom fler tillfrågade innebär att färre finns kvar vars åsikter kan svänga opinionen.

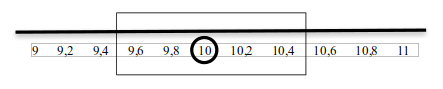
Det är möjligt för en undersöknings resultat att variera utan att det sanna värdet faktiskt har skiftat. Låt säga att vi en månad uppmäter partiets stöd till 10 % och beräknar med hjälp av diverse formler ett konfidensintervall med 99 % säkerhet. Detta får gränserna 9,5 % och 10,5 %. Nästa månad gör vi en ny undersökning och ser att stödet för partiet enligt undersökningen har ökat till 10,2 %. Detta ligger fortfarande inom samma intervall. Alltså kan vi, fastän vi fått ett högre resultat, inte dra någon slutsats om att något verkligen förändrats i världen.

Inte förrän värdet når över 10,5 % eller under 9,5 % kan vi med 99 % säkerhet konstatera att en förändring skett. Detta är oerhört viktigt för de som tolkar statistik, exempelvis vid valundersökningar. Med hjälp av konfidensintervall går det att utläsa hur mycket en undersökning måste variera för att vi med säkerhet ska kunna konstatera att en verklig skillnad faktiskt föreligger.

Det finns olika metoder såsom “Maximum-likelihood-metoden” eller “Momentmetoden” vars syfte är att utifrån varierande mätningar av ett värde uppskatta det sanna värdet så bra som möjligt. Matematiska verktyg som logaritmer används vanligen i den förstnämnda metoden vilket förenklar beräkningarna avsevärt.

Logaritmerna upptäcktes av den skotske matematikern John Napier och var ursprungligen tänkta att förenkla uträkningar inom sjöfarten och bland handelsmännen. De har sedermera letat sig fram till många andra tillämpningsområden av matematik såsom sannolikhetsteorin och statistiken.

Ett konfidensintervall utgår ifrån det uppmätta värdet, vad som har mätts och det totala antalet mätningar. När man talar om människors längder är det mer troligt att få fler resultat kring 170 centimeter än 35 meter. När man talar om hur många sexor som erhålls av ett visst antal tärningskast är sannolikheten noll att antalet blir exakt 2,3 eller 7,6 men det finns en positiv sannolikhet för 2 eller 17 (bara hela tal). De exakta beräkningarna ska jag inte gå in på, men för den intresserade rekommenderas boken Sant eller Sannolikt av Allan Gut.

Ett klassiskt uppskattningsproblem handlar om en man som på sin kvällspromenad räknar ihop totalt fem taxibilar, numrerade 5, 13, 14, 18 och 21. Gissningsvis är bilarna numrerade 1, 2, 3, 4, … och inga två bilar har samma nummer. Hur många taxibilar finns det i så fall i staden? Kanske låter det som ett oviktigt problem, men samma matte användes av de allierade under andra världskriget för att uppskatta antalet stridsvagnar i den tyska armén. Tack vare matematikens generella natur spelar det ingen som helst roll om problemet gäller taxibilar, stridsvagnar eller ens fiskar.

Ett exempel på användningsområde är problemet med att räkna antalet fiskar i en sjö, detta görs med så kallad återfångst. Ett antal fiskar, säg 100, fångas upp ur sjön, märks på något vis och släpps sedan i vattnet igen. Efter en tid fiskas 100 fiskar upp igen. Av dem är kanske 10 märkta. Utifrån detta går det att få rätt bra svar på frågan om hur många fiskar som finns i sjön (eller åtminstone i det området av den).

Exempelvis låter vi vara det totala antalet fiskar i sjön, det som vi vill ta reda på. En dag fångar vi upp 30 fiskar. Vi märker dem och släpper sedan tillbaka dem. Efter en tid går vi återigen ut på fisketur och fångar upp 25 fiskar. Av dessa är 6 st märkta, vilket ger att andelen märkta är . Denna andel torde, liksom när man undersöker partisympati, vara lika stor som andelen hos hela befolkningen. I detta fall utgörs befolkningen av fiskar. Vi vet att det finns 30 märkta av totalt N fiskar, så det ger ekvationen och lösningen:

$$30 / N = {6} / {25} ⇨ N = {25*30} / {6} = 125$$

Svaret är självfallet ungefärligt. För extra säkerhet kan försöket göras om fler gånger. Matematiska modeller finns även för att räkna på hur sannolikt det är att svaret är rätt, och hur mycket det kan tänkas variera. Konfidensintervall spelar in här. Det är nämligen inte säkert att fiskar fördelar sig lika över hela sjön, precis som att numreringen av de tyska stridsvagnarna inte är jämnt fördelad.

Att se samband

Ibland vill man uppskatta ett samband mellan två eller fler olika värden. Antalet cancerfall och antalet mobiltelefonanvändare, till exempel. Något som ofta studeras av bland andra WHO. Ökar antalet cancerfall när användandet av mobiltelefoner ökar? Förmågan att avläsa statistik är oumbärlig för att kunna dra slutsatser, inte bara i detta fall utan också om hur verksam en medicin är (mängden medicin jämfört med hur bra patienterna mår) eller när extra elkraftverk måste användas (mängden förbrukad elektricitet jämfört med datum eller utomhustemperatur).

Här är det viktigt att skilja på korrelation och kausalitet! Det första, korrelation, beskriver hur två saker förändras tillsammans, som att strömförbrukningen ökar när temperaturen minskar. Inget sägs dock om orsakssambandet, kausaliteten. Det kan lika gärna vara en tillfällighet! Kausalitet handlar om orsak - att temperaturens fall leder till kallare hus och mer inomhusvistelser vilket innebär en ökad strömförbrukning. För en sådan slutsats krävs mer än bara statistik.

När en statistisk jämförelse genomförs kan bara korrelation bekräftas, vilket kan missbrukas i det extrema. Antalet McDonald's-anställda har ökat från under hundra personer år 1940 till omkring 400 000 år 2011. Under samma period har antalet människor som varit i rymden ökat från noll till snart 500. Alltså kan vi säga att ju fler människor som reser ut i rymden, desto fler blir anställda på McDonald's. Eller tvärtom, ju fler som McDonald’s anställer, desto fler får resa ut i rymden!

Nej, så kan vi naturligtvis inte säga. Idén känns alldeles absurd. Studeras alla data närmre blir det tydligt att en plötslig ökning av McDonald's-anställda inte direkt åtföljs av en ökning av människor i rymden, och vice versa. Vi hade aldrig någon kausalitet, ty detta kräver en mycket starkare korrelation men även mer tankegångar. Om kausalitet råder bör vi kunna förklara frågan “varför ökar A när B ökar?”, inte bara konstatera att så sker. Vi vet inget som knyter an McDonalds med rymdresor. Däremot kan jag inte säga att det är omöjligt, försök gärna bevisa att jag har fel.

Kausalitet kan också diskuteras på följande vis: Är du sen till en klädrea kan du märka att de vanliga storlekarna har försvunnit. Är de udda storlekarna kvar för att det billigare priset fått de vanligare att gå åt, eller startades rean för att bara de mer ovanliga storlekarna fanns kvar? Eller beror båda händelserna på en tredje, okänd orsak?

Mer om korrelation

Ofta vill man kunna se något matematiskt på ett mer visuellt vis, såsom en geometrisk figur, ett färgmönster eller en linje. Det sistnämnda kan vara en sorts representation (med en del egna användbara egenskaper) av korrelation som kallas regression. Den är bra för att kunna se ett tydligt mönster och kunna förutsäga saker om framtiden. Detta sker ofta i laboratorier men är bara meningsfullt i de fall då kausalitet faktiskt råder.

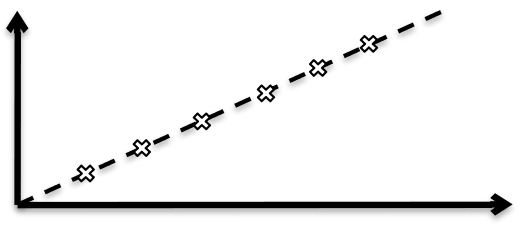
Regressionen illustreras av en linje som beskriver sambandet så noga som möjligt. Att hitta denna linje är ett trivialt problem om alla värden redan följer en linje perfekt:

Oftast föreligger dock en viss felmarginal när mätningar utförs. Det kan gälla mätningar av bromsförmågan hos en bil eller spridningshastigheten av en sjukdom. Att hitta en linje som förutsäger sambandet trots det slumpmässiga felet vid varje mätning är ett mycket svårare problem:

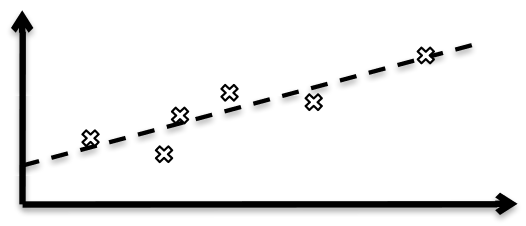
Matematisk regression kan också användas i mer än en variabel, alltså för undersökningar av samband mellan många olika värden. Vi ska inte heller gå in på de matematiska detaljerna här, men jag ger några exempel på hur tekniken används:

• Undersökningar av sambandet mellan hälsa och ålder, bostad, med mera, för att få fram sannolikheten för folk i liknande situationer att leva ett visst antal år till. Detta ger försäkringsbolagen möjligheter att beräkna korrekta livsförsäkringspremier. Samma metod används för att beräkna premier för villa-, bil- och båtförsäkringar.

• Jämförelser mellan hälsa och doseringar av olika mediciner för att kartlägga deras verkan. Förbättrar eller försämrar de hälsan? Beror det på vilka andra läkemedel som samtidigt intas?

• Undersökningar och beräkningar av optimala naturområden. Många olika variabler (antal av olika arter, pH, ljusförhållanden, väder, med mera) kan jämföras med vad som bäst verkar gynna en eller flera djurarter.

Återigen är urvalet viktigast. Enstaka avvikande värden får mindre och mindre konsekvenser ju fler värden som finns tillgängliga. Det finns många andra matematiska verktyg såsom korrelationskoefficient och standardavvikelse som försöker beskriva hur starkt ett samband är och hur mycket olika mätningar varierar.

När det går snett

Jag hoppas att du som läsare blivit lite klokare och lite mer kritisk vad det gäller statistik, men att du fortfarande tror på ämnet. Det är ett oumbärligt verktyg när det sköts rätt

Normalfördelningens graf har ett utseende som påminner om en gammaldags ringklocka och går därför under namnet ”klockkurvan”. Den kan se ut såhär:

Kom också ihåg att skilja på procent och procentenheter! Alltför många blandar ihop dem eller känner inte till skillnaden. Procentenheter gäller alltid delar av allt, medan procent kan gälla delar av delar. Om ett parti får 20 % av rösterna i ett val och 10 % i nästa har deras röster inte sjunkit med 10%. Deras röster har sjunkit med 10 procentenheter! Andelen röster har däremot sjunkit från 20 till 10, alltså hälften, och därmed med femtio procent.