Arkitektur, konstruktion och snickeri

Vetenskap och då även matematik var något som historiskt sågs som mycket mer mystiskt. Bland de som tog det till sin spets var de gamla Pythagoréerna i antikens Grekland; de såg matematiken som något nästintill religiöst, en kraft som låg bakom hela universum.

Pythagoréerna gjorde liksom andra grekiska vetenskapsmän vid denna tidpunkt många viktiga matematiska upptäckter. De lade grunden för dagens matematiska arbetssätt och den syn vi har på ämnet idag: som vetenskapens grund. Deras upptäckter har utvecklats under de millennier som senare passerat och gett upphov till alla de saker vi kommer diskutera framöver.

Matematik har sedan antiken hjälpt till med att på långa avstånd träffa rätt med kanoner. Idag används samma uträkningar för artilleri och prickskytte och ofta inom polisutredningar. Vid mordet av före detta president John F. Kennedy användes geometriska uträkningar och analyser av ljudinspelningar för att räkna ut var skytten var placerad.

Kapitlet kommer inte bara diskutera "vardagsmatte" och hur geometri möjliggör byggnadskonst utan även naturens matte. Mönster som kanske kan förklara matematikens roll i universum och varför ämnet fungerar så bra för att representera och förklara naturen. Det blir en mjukstart inför mer tekniska kapitel.

Emmy Noether, ett namn som ofta figurerar vid högre studier av algebra, var en tysk matematiker som på 1900-talet fastslog kopplingen mellan universums grundläggande krafter och den abstrakta tanken på symmetri. Med symmetri menas i vardagen oftast en spegling av något slag, men termen har en mer abstrakt och generell betydelse som är vanlig inom matematik och annan vetenskap.

Just symmetri är ett exempel på matematisk forskning som senare blir anpassad till många olika områden eftersom den, just för att den är matematisk, är så grundläggande. Det har börjat användas djupare inom partikelfysiken som modell för de allra mest grundläggande byggstenarna i universum. Supersymmetri har blivit del av många olika teorier som berör vilka partiklar som är de allra mest grundläggande, hur många det finns och hur de relaterar till varandra. Symmetri och avvikelser från den är också mycket intressant inom kemin. Molekyler har visat sig kunna ha helt andra egenskaper än sina spegelvändna motparter. Läkemedlet Neurosedyn blev ett ökänt exempel på 1960-talet.

Naturens mönster

Titta på följande talserie och fundera över om det finns något mönster:

1 1 2 3 5 8 13 21 34 55 89 144

Hittar du mönstret? Serien börjar med två ettor, och summerar du ihop dem blir det 2, vilket är nästa tal. De senaste två talen är då 1 och 2, summan av dessa är 3, vilket är nästa tal. Därefter följer 5 och så vidare. Denna serie är mycket berömd och kallas Fibonacciserien efter matematikern Leonardo Fibonacci som på 1200-talet förde in vårt nuvarande talsystem med tio siffror till Europa från öst.

Talserien har visat sig vara mycket intressant att studera då den ofta förekommer i naturen, bland spiraler i allt från snäckor till galaxer. En gran- eller tallkottes fjäll bildar nedifrån och upp spiraler såväl medsols som motsols. Är kotten hel är antalet spiraler lika med Fibonaccitalen 5, 8 eller 13. Ungefär samma sak kan observeras i en solros där antalet spiraler kan vara lika med 34, 55, 89 eller 144 vilka alla är Fibonaccital.

Något annat intressant sker om ett tal i serien delas med det föregående, som $55/34$ eller $89/55$. Ju större tal som används desto närmre kommer kvoten det gyllene snittet, oftast kallat $\phi$, med det ungefärliga värdet 1,61803. Detta är ett tal som, precis som Fibonaccitalen, ofta förekommer i naturen och bland arkitektur. Det figurerar i många antika byggnadsverk, exempelvis förhållandet mellan olika delar av det antika grektiska templet Parthenon.

Cheopspyramiden hade vid sitt upprättande följande mått:

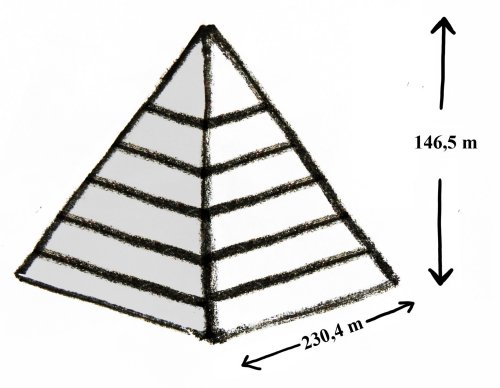
Hos gamla pyramider i Egypten gäller att dubbla sidlängden dividerat med höjden ger ett värde mycket nära pi. Vissa diskuterar huruvida detta tyder på att egyptierna använde stora insikter om cirkelns konstruktion för att bygga pyramiderna. Kanske finns något särskilt vackert med gyllene snittet och pi som vi omedvetet eftersträvar.

Ingenjörer och arkitekter idag behöver mycket matematik för att utföra sina jobb. Det är viktigt att kunna räkna ordentligt från början, det blir tråkigt att bygga upp ett hus, en fabrik eller en skyskrapa och sedan märka att något borde ha gjorts annorlunda. Vad som ligger bakom sådan planering ska vi se på härnäst.

Skala och planering

Det vore mycket arbetssamt att designa ett hus i naturlig storlek då det fordrar mycket stora papper. Processen vore synnerligen opraktisk. Ritningar målas istället upp i någon skala där en meter kan representeras av en centimeter eller millimeter. Mycket små objekt som skruvar eller kugghjul kan visas i en förstorande skala.

Idén kan tyckas elementär men ligger till grund för mycket mer avancerade saker. Allt som ritas upp på en dator- eller TV-skärm kan sägas vara i någon skala i jämförelse med verkligheten. Bildbehandlingsprogram som Photoshop måste ständigt göra intensiva beräkningar när en bild ska visas och i synnerhet när den redigeras.

Bildskärmar och digitala fotografier är uppbyggda av många små enfärgade rutor kallade pixlar, som tillsammans formar en bild liksom rutorna på en kakelvägg. Låt säga att en bild med storleken 3264 x 2448 pixlar ska visas i sin helhet på en datorskärm med upplösningen 1920 x 1080 pixlar. Hela bilden får alltså inte plats och måste skalas ner. Frågan är hur mycket?

För en exakt passform ska bilden krympas med en faktor om:

$${\text"Tillgänglig bredd"}/{\text"Bildens bredd"} = {1920}/{3264} ≈ 0,5882$$

Ett värde vi kan kalla för "krympningsfaktorn". Bildens bredd anpassas till

$$\text"Bredd" ⋅ \text"Krympningsfaktor" = 3264 ⋅ 0,5882 = 1919,88$$

det vill säga mycket nära skärmens bredd om 1920 pixlar. Att det inte blir exakt beror på att vi för läslighetens skull avrundade krympningsfaktorn. Höjden på bilden blir

$$\text"Höjd" ⋅ \text"Krympningsfaktor" = 2448 ⋅ 0,5882 = 1439,9$$

Beskåda! Detta är större än de 1080 pixlar som utgör datorskärmens höjd. Vad ska då ske? Om man tvunget vill att hela bilden ska synas på skärmen samtidigt även i höjdled, som vid en presentation, får en ny krympningsfaktor beräknas som är mindre än den tidigare. De principer vi gått igenom är sanna och gäller i många andra avseenden, egentligen överallt där någon form av zoom är inblandad. Digitalkameror är ett vanligt exempel.

Riktigt såhär enkelt är det egentligen inte heller. En bildskärm består av en begränsad mängd pixlar. Om en mycket högupplöst bild krymps ned på en liten yta kan inte alla pixlar som ingår i bilden visas (det finns helt enkelt inte så många på den lilla ytan). I så fall måste vissa delar av bilden ignoreras, till exempel varannan pixel, så att bilden kan ritas upp där. Just hur detta ska göras för att inte bilden ska se helknasig ut finns det olika metoder för och vissa varianter passar bättre än andra i olika avseenden. Senare i boken kommer vi se hur medelvärden kan användas för att få en blandning av färger hos en större grupp pixlar. Det gemensamma värdet kan användas för att representera hela gruppens färger.

Ett mer sofistikerat exempel är "Seam Carving", en metod utvecklad för att kunna krympa digitala fotografier utan att förlora detaljer. Om en bild är tagen med två hus och ett stort öppet fält emellan är kanske det mest intressanta de två husen och inte det tomma öppna fältet. När bilden ska krympas ned bör således inte alla delar krympas likvärdigt, delar av fältet bör strykas först. Denna metod blir mycket passande.

Hur fungerar den då? Djikstras algoritm, en matematisk metod för att hitta den kortaste eller billigaste vägen mellan två punkter på en karta, används här för att hitta den "billigaste" sträckan i höjd- eller sidled. Med billigaste menas den sträcka som har minst ändringar i färg och kontrast. På husen finns många blandade färger och därmed många detaljer och denna sträcka blir "dyr", medan en grön äng med blå himmel har små förändringar. En sträcka där blir billigare. De "billigare" sträckorna innehåller här alltså färre detaljer och är därmed de som först och främst ska tas bort vid en förminskning.

Att hitta den billigaste sträckan är inget enkelt problem när det finns så många pixlar i bilden och därmed ofantligt många möjliga vägar från en sida till en annan.

Konstruktionsrelaterade problem

När en figur får vissa begränsningar såsom form (ett rektangulärt hus) eller omkrets (begränsad mängd virke till ett staket) kan den anpassas efter angivna krav på olika sätt.

Ska ett staket omsluta en hage kan det vara önskvärt att ytan blir så stor som möjligt. Kanske är den största tillgängliga mängden virke sådan att vi högst får ihop hundra meters omkrets. Kanske måste vi dessutom anpassa oss efter någon specifik form på grund av lagar, markens utseende eller något annat. Låt oss anta att en rektangulär hage är efterfrågad med maximal längd 100 meter. Hur stor yta kan den möjligtvis omsluta?

Låt bredd förkortas $B$ och längd förkortas $L$:

$$\text"(Arean) "\, A = B ⋅ L$$

$$\text"(Omkretsen) "\, ∅ = 2 ⋅ B + 2 ⋅ L = 100$$

Uttrycket för omkretsen kan skrivas om till

$$B = {100 - 2L}/2$$

och sättas in i uttrycket för arean vilket ger

$$A = {100 - 2L}/2 ⋅ L = 50L - L^2$$

Vi försöker hitta värdet för längden som ger den största möjliga arean. Det visar sig (med hjälp av det matematiska verktyget derivata) att denna längd är 25 meter. Där har vi det! När vi vet längden på denna sida och den totala omkretsen kan bredden också räknas ut och det visar sig att denna också blir 25 meter vilket gör hagen kvadratisk.

I vissa fall kan det finnas andra begränsningar eller önskemål om andra former, kanske en uteplats som ska vara fem- eller sexhörnig med en begränsad takhöjd. För att slippa behöva söka bygglov måste byggnaden uppfylla vissa storlekskrav.

Metoderna förblir desamma även om förhållandet ibland är det omvända: att ytan kostar mycket pengar och en inhägnad eller byggnad ska anpassas efter en minsta möjliga areakostnad. Av dessa anledningar blir skyskrapor mycket vanliga i större städer.

I vilket fall som helst är det matematiska kunskaper och erfarenheter av dessa som är bra hjälpmedel vid bra beslutsfattande. Beslutsteori, ett stort tvärvetenskapligt område inom filosofin och matematiken är också ofta tillämpat. Detta område försöker ge uttryck för hur optimala beslut fattas.

Den figur som har minst yta i förhållande till den volym den omsluter är klotet och av denna anledning har många små organismer och celler denna form. Den blir effektivast eftersom minsta mängd material används för att konstruera cellväggarna som omsluter och skyddar den. Även naturen räknar matte. Ett annat synsätt är att cellväggarna konstrueras på så vis på grund av universums egenskaper. Matematiken får då istället rollen som en förklarare, en medlare av information. Det redskap som låter oss förstå såväl hur som varför.

Konstruktion av broar fordrar många beräkningar för att försäkra alla inblandade om att utseendet och valet av material garanterar att bron håller för en viss vikt (motsvarande ett visst troligt antal lastbilar eller människor). Olika förutsägelser om vid vilka tider maximal trafiknivå uppnås och hur hög denna nivå är uträttas också matematiskt, på sätt som diskuteras i kapitlet Statistik. Tunnelborrning har samma matteberonde: arbetet börjar oftast från två olika håll och endast med geometrin kan de inblandade försäkra sig om att de två delarna faktiskt kommer mötas i mitten.

Industrirobotar

En industrirobot som förflyttar och monterar delar kan bestå av en komplicerad robotarm med leder i olika riktningar, positionerad på en roterande platta. Att få robotarmens "hand" att röra sig i en rät linje är då ingen enkel uppgift, eftersom en led kanske inte har så mycket svängrum. Försök hålla en hand framför dig och röra den rakt framåt, inte i sidled eller i höjdled. Du märker att du inte kommer lyckas genom att bara röra handleden, du måste kombinera förflyttningar av hela armen: handleden, armbågen och axeln, för att få handen att röra sig rakt.

Detta är något som gärna eftersträvas även i robotsammanhang: kontrollerade rörelser längs olika fasta banor genom kombinationer av rörelser i olika vinklar. En matematiker tar då fram formler för att beskriva hur dessa rörelser kan utföras, som sedan används för att programmera roboten. En intressant fråga kan också vara hur långt robotarmens hand kan förflyttas i olika riktningar. Står du still och för din hand rakt framåt kan du omöjligen nå tre meter bort, hur du än vinklar din armbåge och axel. Dessa typer av problem, när maximala eller minimala gränser hos ett värde ska hittas, brukar i matematiken kallas extremvärdesproblem.

För att lösa dessa extremvärdesproblem används formler och kunskap inom geometri och trigonometri som matematiker utvecklat under årtusenden. Att se hur, eller ens om, roboten kan föra sin hand från en plats till en annan är en något enklare uppgift. Låt oss titta på den. Ett sätt att uttrycka en rörelse som innefattar ett avstånd och en vinkel på ett matematiskt vis är med vektorer som här illustreras av pilar.

Vi vill flytta handen från den vänstra punkten till den högra:

Robotarmen har tre leder och kan justera handens position i varsin riktning. Om vi med pilar ritar upp hur de var för sig påverkar rörelsen för handen, kan vi få något som nedan:

Genom att förflytta oss olika långt längs lederna produceras olika långa pilar. Vid rotation bevaras pilens längd men pekar istället i en annan riktning. Summan av alla dessa rörelser får vi om vi summerar alla vektorer - alltså "klistrar ihop" pilarna efter varandra medan vi fortfarande bevarar riktningen. Då ser vi:

Det vill säga ett sätt att röra robotens hand från den ena punkten till den andra, exempelvis från en hög med fordonsdelar till den bil som är under konstruktion. När dessa vektorer uttrycks matematiskt ger de bra verktyg för att lösa problemet med hur dessa kombineras för att nå en specifik plats eller följa en specifik väg. Detta matematiska område kallas främst linjär algebra. Datorer kan inte tänka i pilar, robotar behöver den matematiska notationen.

Inom ämnet reglerteknik försöker man ta fram matematiska uttryck som automatiskt kan reglera något elektroniskt system. Det kan gälla hur mycket farthållaren i en bil ska gasa för att uppnå vald hastighet. Mer acceleration önskas om nuvarande hastighet är 50 km/h och önskad hastighet är 90 km/h, men en mycket liten förändring fordras om nuvarande hastighet är 89 km/h. En ekvation måste även kunna reagera olika beroende på hur mycket vägen lutar vilket inte underlättar problemet.

Själva förflyttningen av robotarmen är inte enkelt utförd. Ofta är det någon elektrisk spänning som ställs in som får armen att röra sig till önskat läge. Är spänningen för svag blir rörelsen långsam, men är spänningen för stark svänger armen för fort och förbi önskad position. Armen måste då stanna och vridas tillbaka vilket fördröjer arbetet. Vilken kurva ska spänningen följa för att förflyttningen går så snabbt som möjligt? Efter att ha läst boken hittills är det nog inte förvånande att även denna fråga besvaras med matematiska medel.

Övrigt

Det finns mycket annat att ha i åtanke när byggnader eller fordon konstrueras.

• Luftflödet och ventilationen: Är det hälsosamt att befinna sig i lokalen? Speciellt viktigt är det i fabriker. Relaterat till detta är Navier-Stokes ekvationer som beskrivs i kapitlet om olösta problem.

• Ljudnivåer: Hur många befinner sig i en lokal och hur hög ljudnivå kan en person eller maskin där tänkas uppbringa? Hur hög ljudnivå blir det då gemensamt, blir det skadligt högt på någon plats?

• Ljusstyrka: Hur ljust blir det genom fönstren och längs vilka vinklar skiner solen? Hur kommer ljuset att sprida sig genom rummen, blir några områden för mörka?

• Hållbarhet: Hur är vikter och material fördelade? Är slutprodukten hållfast och säker? Hur skulle byggnaden klara sig i starka vindar eller jordbävningar? Klarar en vattendamm av påfrestningen från den sjö eller flod den dämmer upp?

Arkitekter och byggnadsingenjörer har mycket utbildning inom mer än matematik för att finna svar på dessa frågor, men sakerna studeras och modelleras med matematisk metodologi. Det är oftast det mest effektiva sättet att uttrycka saker på ett koncist vis för att underlätta förutsägelser och testa nya metoder.

På så vis kan generella metoder och konstruktionsregler motiveras och läras ut utan högre mattekunskaper. För att förstå dem mer i detalj och kunna utveckla dem är dock mattekunskaperna ett måste.